Nonorientable Minimal Surfaces

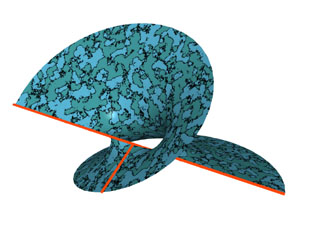
The red curves are straight lines on the surface.

Nonorientable Minimal Surfaces |
||
|---|---|---|
|
|
In general, the interest in mimimal surfaces is focussed on complete embedded surfaces. However, embeddedness is impossible to achieve for complete nonorientable surfaces. Nevertheless, this is a very interesting class of surfaces, for several reasons. One reason is technical: Minimal surfaces come in three stages of complexity: The simplest ones exist just by symmetry. The modestly difficult surfaces exist by solving some low-dimensional period problem. And the most complicated arise from these by inductive procedures or desingularization techniques. As the supply of modestly difficult surfaces is rather small, any new example in this class with not too complicated topology is interesting. | |
| To the right, you can see Meeks's Möbius strip. It is in fact part of a punctured projective plane. The black curves are a circle and a straight line lying on the surface. |  |
|
| It is a suprising phenomenon that some well-known non-embedded minimal surfaces with relatively
small absolute total curvature are half-embedded, that is, there is a reflective symmetry so that a
fundamental piece with respect to the symmetry is embedded. Enneper's surface is a simple example,
and another beautiful example is Lopez' Klein bottle, the unique non-orientable surface of least absolute
total curvature. The red curves are straight lines on the surface. |
 |
|
| Another example of this kind is a singly periodic nonorientable surface with a singular vertical line. All its ends ar planar, and a fundamental pice arises from solving a Plateau problem in the wedge of a slab. It is conceivable that this surface arises as a limit of singly periodic surfaces of the Callahan-Hoffman-Meeks type, when more and more handles are added. Or, the latter surfaces with high genus could possibly be obtained by desingularizing a la Kapouleas the vertical coordinate line of the surface to the right. |  |
|