Helicoidal Minimal Surfaces
These pages survey results obtained by Martin Traizet and myself, see our preprint.
The study of minimal surfaces with helicoidal ends was originally motivated by the desire to construct a genus g helicoid as the limit of screw-motion invariant minimal surfaces with genus g in the quotient for increasing twist angle. While this limit is hard, it is easier to understand the limits of such surfaces for decreasing twist angle.We expect that these surfaces must degenerate in a very peculiar way. In fact, by starting at certain degenerate situations, we can prove the existence of minimal surface families that are invariant under screw motions and have helicoidal ends.
.jpg)
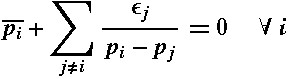
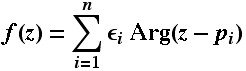
cyc1.jpg)