The Costa Minimal Surface



The Costa Minimal Surface |
||
|---|---|---|
|
|
The Costa Surface, found in 1984, provides an example of an embedded minimal surface with the topology of a thrice punctured torus. This single surface has triggered an enormous amount of research, resulting in many new surfaces, theorems, and open conjectures. | |
 |
||
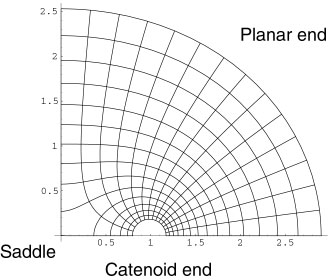
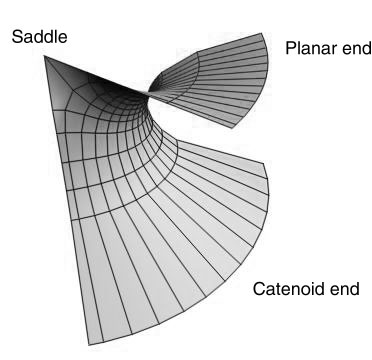
| The Costa surface consists of eight congruent pieces, which are pulled apart slightly in the right figure. Each of the eight pieces is the conformal image of the first quadrant under Schwarz-Christoffel maps. The figure below illustrates the chosen parametrization. You can also view and download a fairly well documented Mathematica notebook which uses this parametrization to draw Costa's surface. |  |
|
 |
 |
|
| The Costa surface is originally defined on a square torus. It admits a deformation (Hoffman and Meeks) where the planar end becomes catenoidal. These surfaces are then defined on arbitrary rectangular tori. |  |
|