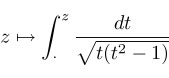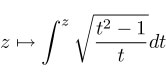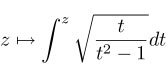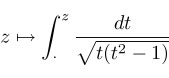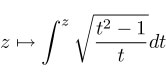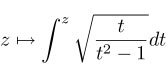| |
Schwarz-Christoffel Maps |







|
The Schwarz-Christoffel formulas gives an integral expression
which maps the upper half plane conformally onto a polygonal shaped domain.
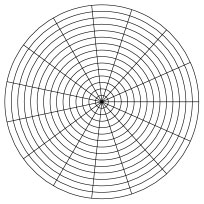
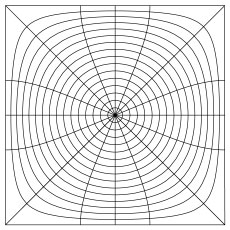
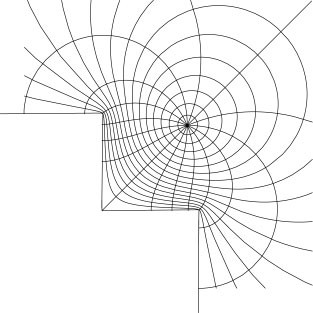
As an example, consider the map to the right which maps the upper half plane conformally to a square: |
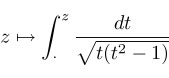 |
 |
 |
| What does this have to do with minimal surfaces? Well, in the Weierstraß representation of many
important minimal surfaces, the 1-forms G dh and 1/G dh very often are Schwarz-Christoffel integrands.
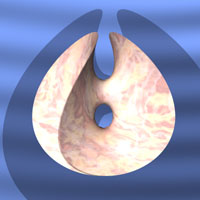
One of the simplest examples is the Chen-Gacksttater surface, a minimal torus with one Enneper type end. |
 |
| One quarter of the surface is conformally the upper half plane. If we map this upper half plane not into euclidean space but instead to a polygonal domain, using first G dh as a Schwarz-Christoffel integrand, we get the following zigzag shaped domain: |
 |
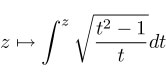 |
 |
| Using 1/G dh instead, we obtain a complemantary zigzag. Angles at corresponding vertices fit togther to 360 degrees. |
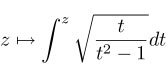 |
 |
| The important feature of these period domains is now that they can help
understanding the period problem. For instance, higher genus Chen-Gackstatter surfaces correspond
to zigzags with more vertices. The period problem for these surfaces can be reduced to the seemingly
unrelated question whether there is a zigzag which divides the plane into two regions which are
conformal by a map mapping corners to corners. |