Dihedral Symmetry

	Dihedral Symmetry
	Many known relatively simple minimal surfaces are symmetric with respect to reflections about the vertical coordinate planes. A fundamental piece of the surface lies in a right angled coordinate wedge, and the surface cuts the boundary othogonally. In all known cases, this fundamental piece can be deformed continously to lie in any wedge with smaller angle. If this smaller angle is an integral fraction of 360 degree, reflecting at the boundary planes of the wedge gives a new closed minimal minimal surface with a higher order of symmetry. Below to the left you can see such a surface patch in a 2pi/5 wedge, and the complete surface to the right. The actual symmetry group of the surface is larger, and it is a matter of taste how large a fundamental piece one is using. The order 5 rotational symmetry of the surface is in this case very well visible.

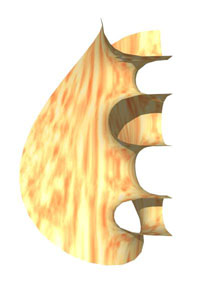
	To the right is a picture of Scherk's singly periodic minimal surface with a rotational symmetry group of order 9 about the z-axes. The surface continues infinitely up and down with translational copies of itself.
	Finally, here is a Costa-Hoffman-Meeks surface which is symmetric about the z-axes by a rotation of order 20. Observe how planar the surface becomes near the fixed points of the high order symmetry.