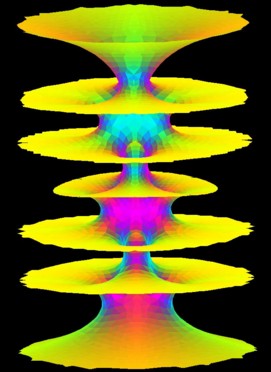
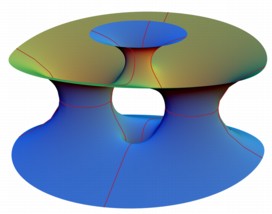
The Hoffman-Meeks conjecture
The Hoffman-Meeks conjecture claims that a complete embedded minimal surface of genus g can have at most g+2 ends. To the right is an example with genus 5 and 7 ends, derived from Costa's surface. Below is an example with genus 1 and 4 ends which is not embedded as a complete surface.